CL Newsletter, May 2023 - More With Patterns

Resources CL Newsletter Archive
1

Of all the newsletter requests we receive, sharing more information about patterns in CL has been by far the most popular. We’ve touched on the pattern library in the past, sharing general advice and ways to avoid possible pitfalls, but this month, we want to take a deeper look at one of our favorite patterns and how you can use it.

functionCall

functionCall is a pattern that identifies a function and its arguments. For example:
f(x,y,y)
Function: f
Arguments: x, y, z g(3x+1)
Function: g
Argument: 3x+1

Getting started

  1. The functionCall pattern is used without any arguments. As long as you’re not building anything around it, patterns.functionCall is all you need to parse a function.
  2. Once you parse a function you can extract the following:
  • identifier
  • n (the number of arguments)
  • nth (the argument in the nth place)

For example, the script patterns.functionCall.parse(f(2,3,x)) gives you the following:

  • identifier: f
  • n: 3
  • nth(1): 2
  • nth(2): 3
  • nth(3): x

What can you use it for?

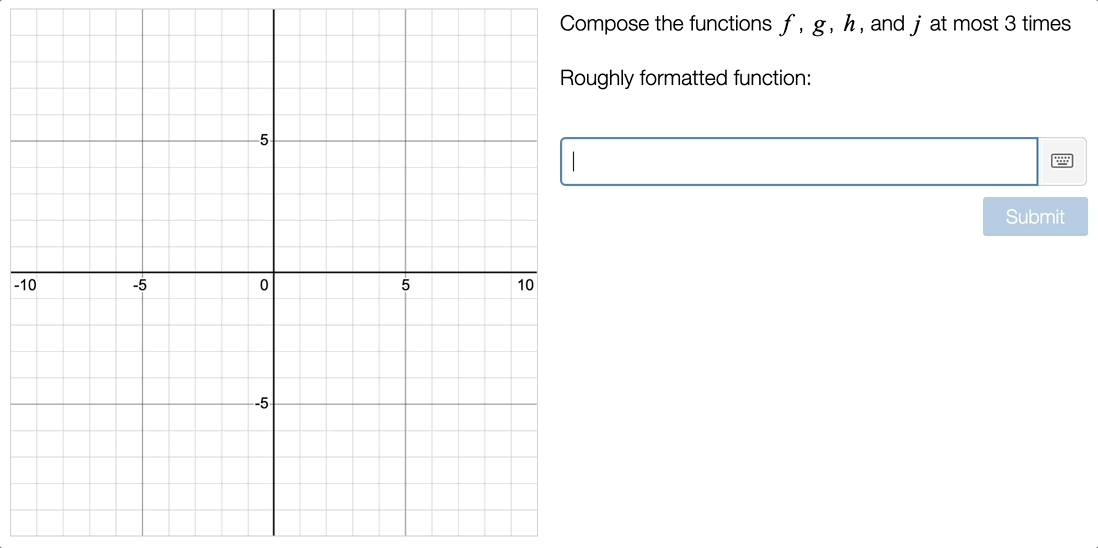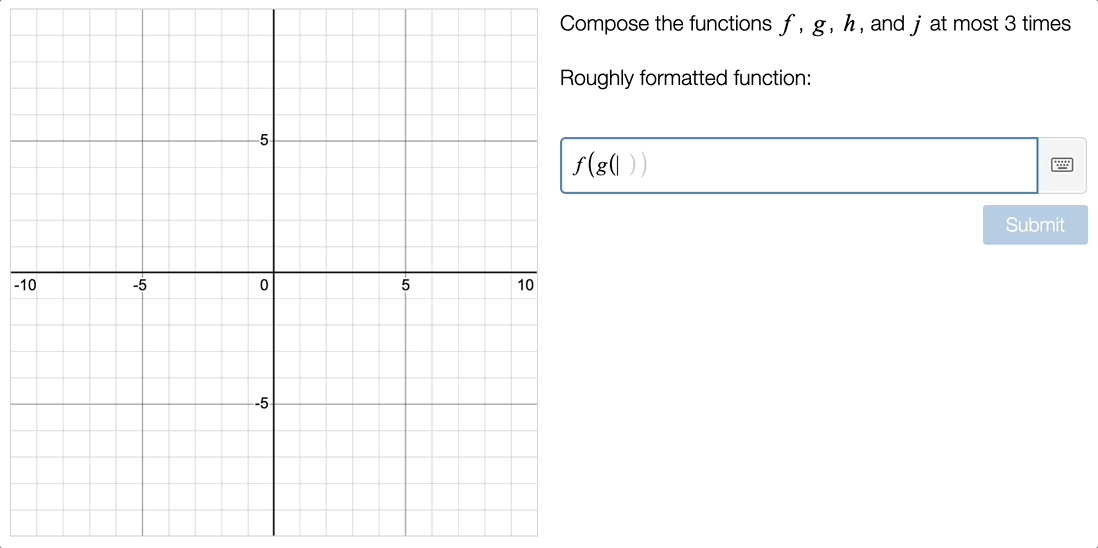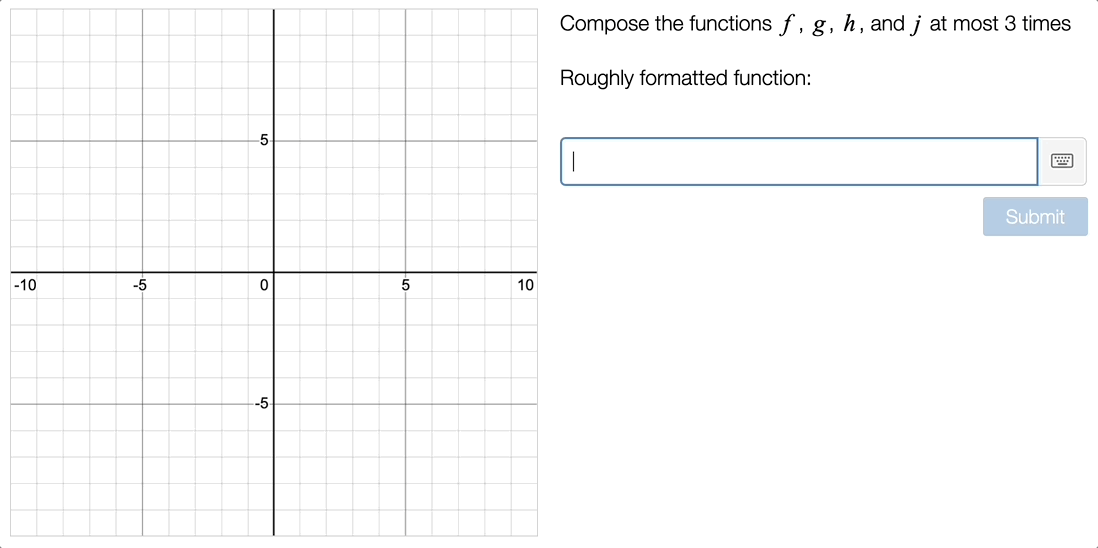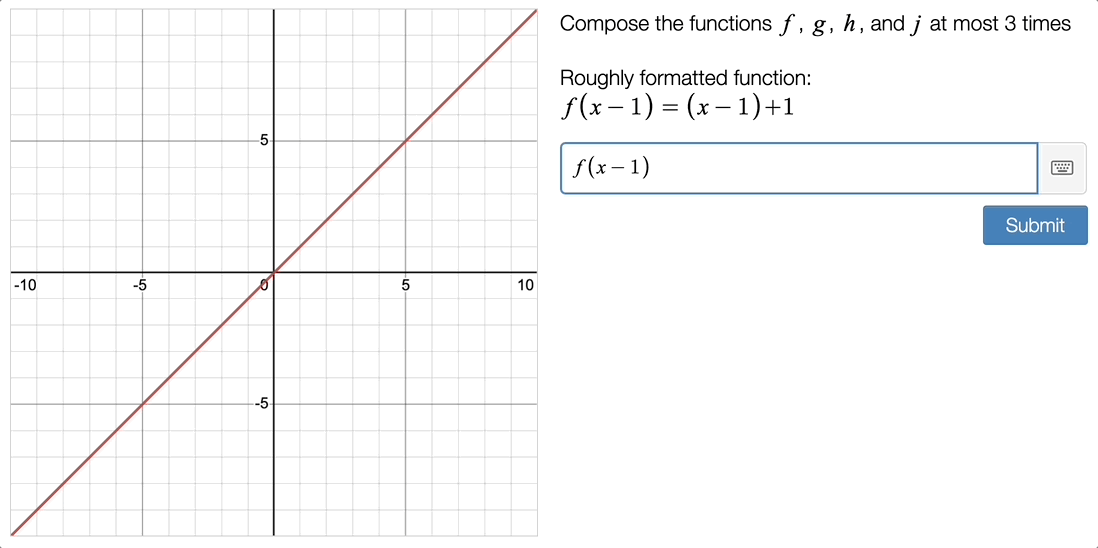
Function Compositions

Students can explore function compositions using function notation. Parse the initial input and then the arguments of each previous function, then stitch the functions together using whatever method you want.

“Other” functions

Other functions, like sin, cos, tan, and even log, can be parsed. The only drawback is that students will need to use parentheses with the functions (e.g., log3 won’t work but log(3) will). With logarithms, you can even parse the base as the second argument.

??? :exploding_head:???

Because arguments are separated by commas, we can, with a little trickery, identify a surprising variety of inputs using functionCall.

STUDENT ENTERS A LIST

Student input: 1, 2, 3, 4
Script: functionCall.parse (f(${input}))
Extractable Information:
identifier: f
n = 4
nth(1) : 1
nth(2): 2
nth(3): 3
nth(4): 4

3-D COORDINATES

Student input: (x,y,z)
Script: functionCall.parse(f${input})
Extractable Information:
identifier: f
n = 3
nth(1) = x
nth(2) = y
nth(3) = z

2-D VECTORS

Student input: <x,y> (using inequalities)
Script: functionCall.parse(f(0${input}0))
Extractable Information:
Identifier: f
n = 2
nth(1) = 0<x
nth(2) = y>0
To get the values, you’ll have to do a little more work. Here’s some condensed code. To see the whole thing at work, check out the sample activity below.
Component 1: parseInequality(nth(1)).rhs
Component 2: parseInequality(nth(2)).lhs

3-D VECTORS

Student input: <x,y,z> (using inequalities)
Script: functionCall.parse(f(0${input}0))
Extractable Information:
Identifier: f
n = 3
nth(1) = 0<x
nth(2) = y
nth(3) = z>0
You’ll also have to do a little more work here, but just for components 1 and 3.
Component 1: parseInequality(nth(1)).rhs
Component 3: parseInequality(nth(3)).lhs

Need a closer look at any of these examples? Check out this sample activity.

Ensuring valid inputs

One risk of using a tool like this to do something it wasn’t intended to do is that it might improperly parse a student’s input. Make sure to check every part of the extracted information and provide the proper error messaging and blocking so that students know how to correct their response.