This is a trivial question but I haven’t found the answer in the documentation. In the 3D graphing calculator, I can move a slider from Orthographic to Perspective but how far is the viewpoint from the origin at the most extreme Perspective view. For example, if the scales are set to say be all -100 to +100, would the viewpoint be say 200 units from the origin?
Yes I think so, it would be 2 * distance
I think that the question may not be well posed …
I don’t think that there’s an answer to the question because
the reference system used to calculate the projections is not the
reference system we see in the 3D calculator … there is a 3D
reference system where all the objects live including as an object our graphing space.
So the units we see do not correspond to the units in the projection space that the programmers used.
I guess that is what he meant by “trivial question”
By “trivial”, I meant that I assumed it would be in the documentation somewhere but that I just hadn’t found it while other more experienced users could tell me where to look.
There isn’t much information on the viewport I think (I’ve never searched it up before). You can maybe look for yourself on the help page.
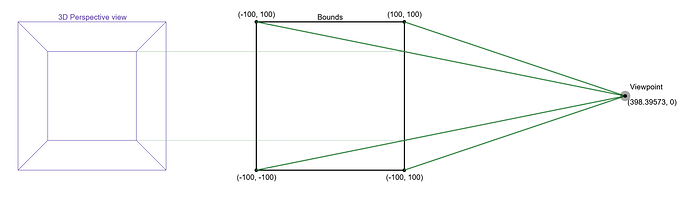
In the end, I took a pragmatic approach, I took a screenshot of the bounding box, found the pixel locations then solved for the viewpoint coordinates, My numbers are not exact because the lines are a little fuzzy so to the nearest pixel but the calculation says that for graph bounds of -100 to +100, the distance from the origin comes out at 398.4 so I suspect it is actually 400 units or as you say 2 times the length of the bounding edges.
Thanks for the responses @NTMDev and @Guzman_Tierno.
This may help others if they need to know this information. The image on the left matches the bounds cube for all axes running -100 to +100 if the the slider is slid fully to the right to select “Perspective”. The image on the right shows the inferred location of the viewpoint. There may be some rounding for the pixel locations so the location might be at exactly (400,0).